浅谈数论

引子

符号的规定

$\forall x \in \Z,y \in \N^+$ $k,r$ $x = ky + r(k \in \Z,r \in \N 且 r\lt y)$ $r = x \mod y$ ,称为"x 取余 y"。
显然,“取余”运算满足以下性质:
- $x\mod y=(x+y)\mod y$
- $x\mod y=x (0 \leq x \lt y)$
$\forall x,y \in \Z,m \in \N^+$ $(x \mod m) =(y \mod m)$ $x \equiv y (\mod m)$ ,称为"x,y 同余 m" 显然“同余”运算满足以下性质:
- $x\equiv y(\mod m)$ $x + k\times m\equiv y + j\times m(\mod m ) \ \ (k,j\in \Z)$
$\forall x,y \in \Z$ $gcd(x,y)$ 为 x,y 的最大公约数
$gcd(x,y)$ 满足以下性质:
1. $y\geqslant0 , gcd(x,y)= \begin{cases} gcd(y,x\mod y)\,, \quad &y\ne 0 \\ x,\quad &y=0 \end{cases}$ ¹
2. $\forall x,y , gcd(x,y)=gcd(-x,y)=gcd(x,-y)=gcd(-x,-y)$
$gcd(x,y)=1$ $x,y$ 互质
$gcd(x,y)=x$ $x$ $y$ $y$ $x$ $x\mid y$ $x\nmid y$

引例

一个正整数，除以三余二，除以五余二，除以七余三，问这个数最小是多少？

二元一次方程的整数解

定义&性质

$ax + by = c \quad (a,b \in \N,c \in \Z)$ 的方程，称为二元一次整数方程

显然，有以下性质：

$gcd(a,b)\nmid c$ ， $x,y$ 无整数解 ²
$x_0,y_0$ $\begin{cases} x=x_0+bt\\ y=y_0-at \end{cases} (t \in \Z)$ ³

step1:恒等变形

$ax + by = c$

$a^\prime=\frac{a}{\gcd(a,b)},b^\prime=\frac{b}{\gcd(a,b)},c^\prime=\frac{c}{\gcd(a,b)}$
$a^\prime x+b^\prime y=c^\prime$ $a^\prime,b^\prime互质$ $\therefore ax+by=c \iff a^\prime x+b^\prime y=c^\prime (a,b互质)$ (人话:约分)

step2:倍比变形

$① ax + by = c$ $a,b$ 互质）

$ax^\prime+by^\prime=1$ $b$
$②ax^\prime c+by^\prime c=c$ $\begin{cases} x=x^\prime c\\ y=y^\prime c \end{cases}$ $ax+by=1(a,b互质)$ 即可

step3:递归求解-递

$ax + by = 1\;(a,b互质)$ $\because a,b互质$ $\therefore ax + by = 1 \iff ax + by = \gcd(a,b)$ $a^\prime,b^\prime$ $a,b$ $a^\prime x + b^\prime y = \gcd(a^\prime,b^\prime)$ $a^\prime = b,b^\prime = a\mod b$

以此类推，不断进行辗转相除

$a^{\prime\prime} x + b^{\prime\prime} y = \gcd (a^{\prime\prime},b^{\prime\prime})$ $a^{\prime\prime\prime} x + b^{\prime\prime\prime} y = \gcd(a^{\prime\prime\prime},b^{\prime\prime\prime})$ $\gcd$ $b^{\prime\prime\prime...}$ 总会等于 0 $a^{\prime\prime\prime...}x + 0\times y = a^{\prime\prime\prime...}$ $x = 1$ $y$ 为任意整数,为了计算方便,令其为 $0$

step4:递归求解-归

$x=1,y=0$ $a',b'$ $a,b$ $x,y$ $a^\prime=b,b^\prime=a \mod b$ 了，所以能否通过它找出关联呢？(你猜如果没关系那我为什么要令:) )

$x_{n},x_{(n+1)},y_{n},y_{(n+1)}$ $ax_{n}+by_{n}=\gcd(a,b)$ $bx_{(n+1)}+(a\mod b)y_{(n+1)}=\gcd(b,a\mod b)$ $\gcd$ $\gcd(a,b)=\gcd(b,a \mod b)$ $ax_{n}+by_{n}=bx_{(n+1)}+(a\mod b)\times y_{(n+1)}$ $ax_{n}+by_{n}=bx_{(n+1)}+(a- \lfloor\frac{a}{b}\rfloor \times b)\times y_{(n+1)}$ $ax_{n}+by_{n}=bx_{(n+1)}+ay_{(n+1)} - \lfloor\frac{a}{b}\rfloor b y_{(n+1)}$ $ax_{n}+by_{n}=a y_{(n+1)}+b[x_{(n+1)}- \lfloor \frac{a}{b}\rfloor y_{(n+1)}]$

step5:整理

只需要将 1、2、3、4 步骤结合即可得出答案

$56x+29y=4$

\begin{matrix} 有 ： \\ 56 x_{1} + 29 y_{1} = 1 (x = 4 x_{1}, y = 4 y_{1}) \\ 29 x_{2} + 27 y_{2} = 1 \\ 27 x_{3} + 2 y_{3} = 1 \\ 2 x_{4} + y_{4} = 1 \\ x_{5} = 1 \\ x_{5} = 1, y_{5} = 0 \\ x_{4} = y_{(4 + 1)} = 0, y_{4} = (x_{(4 + 1)} - ⌊ \frac{2}{1} ⌋ \times y_{(4 + 1)}) = 1 \\ x_{3} = y_{(3 + 1)} = 1, y_{3} = (x_{(3 + 1)} - ⌊ \frac{27}{2} ⌋ \times y_{(3 + 1)}) = - 13 \\ x_{2} = y_{(2 + 1)} = - 13, y_{2} = (x_{(2 + 1)} - ⌊ \frac{29}{27} ⌋ \times y_{(2 + 1)}) = 14 \\ x_{1} = y_{(1 + 1)} = 14, y_{1} = (x_{(1 + 1)} - ⌊ \frac{56}{29} ⌋ \times y_{(1 + 1)}) = - 27 \\ x = x_{1} \times 4 = 56, y = y_{1} \times 4 = - 108 \end{matrix}

$\therefore\begin{cases} x=56\\ y=-108 \end{cases}$ $56x+29y=4$ 的一组解

$\therefore\begin{cases}x=56+29t\\ y=-108-56t \end{cases}为通解$

代码实现

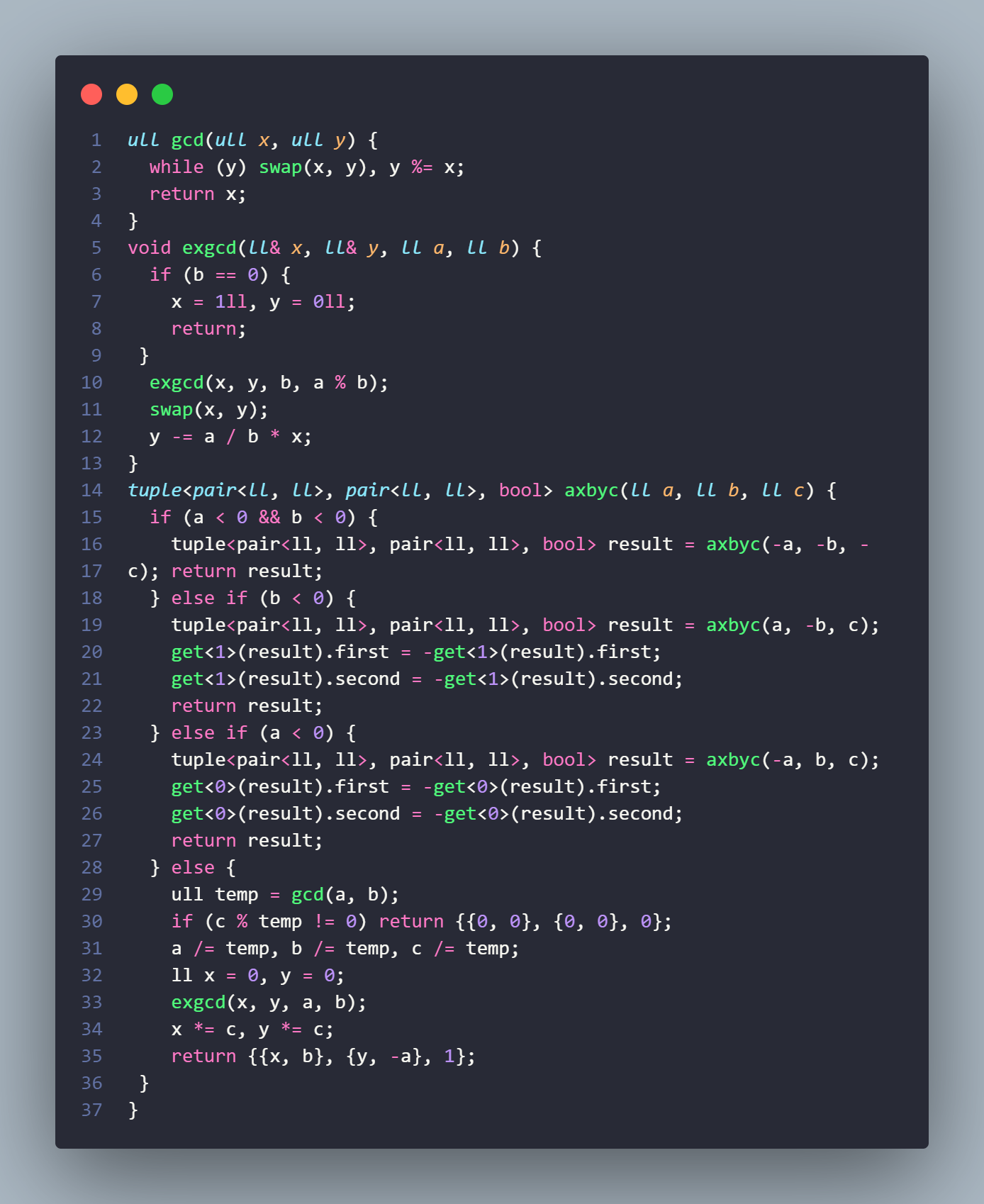
线性同余方程

定义与性质

$ax\equiv b(\mod c)(a,b\in \Z,c \in N^+)$ 的方程，称之为线性同余方程（求解最小非负整数 x）

$(a \mod c)x+cy=b(a,b\in \Z,c \in N^+)$ ⁴ $\begin{cases}x=x_0+ct\\y=y_0-at \end{cases}或x,y\notin \Z$ 的解

$x=x_0+ct$ $\therefore x=x_0 \mod c$

$5x\equiv70(\mod 25)$

\begin{matrix} 5 X \equiv 70 (\mod 25) \Leftrightarrow 5 X + 25 Y = 70 \\ X + 5 Y = 14 \\ x + 5 y = 1 \\ 5 x_{0} + y_{0} = 1 \\ x_{1} = 1, y_{1} = 0 \\ x_{0} = 0, y_{0} = 1 \\ x = 1, y = 0 \\ X = 14 \mod 5 = 4 \end{matrix}

中国剩余定理（孙子定理）

定义

$\begin{cases}x\equiv a_1(\mod m_1)\\x\equiv a_2(\mod m_2)\\ \cdots\\x\equiv a_n(\mod m_n) \end{cases}$ 的方程组，称之为线性同余方程组

$(m_1, m_2, \cdots, m_k)$ 互质时，我们可以使用中国剩余定理 (Chinese Remainder Theorem)进行求解。

核心思想(易得，这里不作证明)

\begin{matrix} x_{0} = \sum_{i = 1}^{n} u_{i}, 其 中 u_{i} 满 足 {\begin{cases} u_{i} \equiv 0 (\mod m_{1}) \\ u_{i} \equiv 0 (\mod m_{2}) \\ \dots \\ u_{i} \equiv a_{i} (\mod m_{i}) \\ \dots \\ u_{i} \equiv 0 (\mod m_{n - 1}) \\ u_{i} \equiv 0 (\mod m_{n}) \end{cases} \\ x = x_{0} + k \prod_{i = 1}^{n} m_{i} (k \in Z) \end{matrix}

具体实现

\begin{matrix} 令 M = \prod_{i = 1}^{n} m_{i}, M_{i} = \frac{M}{m_{i}}, 此 时 \forall 1 ⩽ j ⩽ n 且 j \neq i, m_{i} ， 满 足 M_{i} u_{j} \equiv 0 (\mod m_{j}) \\ 接 下 来 只 需 要 解 方 程 M_{i} v_{i} \equiv a_{i} (\mod m_{i}) ， 此 时 ， u_{i} = M_{i} v_{i} \end{matrix}

举例

$\begin{cases}x\equiv 2(\mod 3)\\x\equiv 3(\mod 5)\\ x \equiv 2 (\mod 7) \end{cases}$ ，

\begin{matrix} 35 u_{1} \equiv 2 (\mod 3) \\ u_{1} = 1 \\ 21 u_{2} \equiv 3 (\mod 5) \\ u_{2} = 3 \\ 15 u_{3} \equiv 2 (\mod 7) \\ u_{3} = 2 \\ x_{0} = 35 \times 1 + 21 \times 3 + 15 \times 2 = 128 \\ x = x_{0} \mod 105 = 23 \end{matrix}

$\therefore x=23$

代码

1 证明：当

y = 0

$y = 0$ 时，

x

$x$ 和

y

$y$ 的公因数就是

x

$x$ 的因数，而最大公因数就是

x

$x$ 本身，所以

g c d (x, 0) = x

$gcd(x,0) = x$ 。
当

y \neq 0

$y \neq 0$ 时，设

x = k y + r

$x = ky + r$ （

k \in Z

$k \in \Z$ ，

r \in N

$r \in \N$ 且

r < y

$r < y$ ），即

r = x \mod y

$r = x \mod y$ 。
设

d

$d$ 是

x

$x$ 和

y

$y$ 的公因数，即

x = m d

$x = md$ ，

y = n d

$y = nd$ （

m, n \in Z

$m,n \in \Z$ ），则

r = x - k y = m d - k n d = (m - k n) d

$r = x - ky = md - knd = (m - kn)d$ ，所以

d

$d$ 也是

y

$y$ 和

r

$r$ （即

x \mod y

$x \mod y$ ）的公因数。
反之，设

d

$d$ 是

y

$y$ 和

x \mod y

$x \mod y$ 的公因数，即

y = p d

$y = pd$ ，

x \mod y = q d

$x \mod y = qd$ （

p, q \in Z

$p,q \in \Z$ ），因为

x = k y + (x \mod y) = k p d + q d = (k p + q) d

$x = ky + (x \mod y) = kpd + qd = (kp + q)d$ ，所以

d

$d$ 也是

x

$x$ 和

y

$y$ 的公因数。
这表明

x

$x$ 和

y

$y$ 的公因数集合与

y

$y$ 和

x \mod y

$x \mod y$ 的公因数集合相同，那么它们的最大公因数也相等，即

g c d (x, y) = g c d (y, x \mod y)

$gcd(x,y) = gcd(y,x \mod y)$ 。 ↩

2 证明：对于方程

a x + b y = c

$ax + by = c$ ，假设

x, y \in Z

$x,y\in \Z$ ，因为

g c d (a, c)

$gcd(a,c)$ 是

a

$a$ 和

c

$c$ 的最大公因数，所以

a = m \times g c d (a, c)

$a = m\times gcd(a,c)$ ，

c = n \times g c d (a, c)

$c = n\times gcd(a,c)$ （

m, n \in Z

$m,n \in \Z$ ）。则有

m gcd (a, b) x + n gcd (a, b) y = c

$m\gcd(a,b)x+n\gcd(a,b)y=c$

gcd (a, b) (m x + n y) = c

$\gcd(a,b)(mx+ny)=c$
当

m x + n y = \frac{c}{gcd (a, b)}

$mx+ny=\frac{c}{\gcd(a,b)}$

∵ m, n ， x ， y \in Z

$\because m,n，x，y \in \Z$

∴ m x + n y \in Z

$\therefore mx+ny \in \Z$
此时若

gcd (a, b) ∤ c

$\gcd(a,b) \nmid c$ ，则

m, n ， x ， y \notin Z

$m,n，x，y \not \in \Z$ ，与假设矛盾，故

x, y \notin Z

$x,y\not \in \Z$
结论：若

g c d (a, b) ∤ c

$gcd(a,b)\nmid c$ ， $x,y$ 无整数解 ↩

3 证明：若

x_{0}, y_{0}

$x_0,y_0$ 是该方程的一组解，则有

\begin{matrix} a x_{0} + b y_{0} = c \\ a x_{0} + a b t - a b t + b y_{0} = c \\ a (x_{0} + b \times t) + b (y_{0} - a \times t) = c \\ ∴ {\begin{cases} x = x_{0} + b t \\ y = y_{0} - a t \end{cases} \end{matrix}

$ax_0+by_0=c\\ ax_0+abt - abt + by_0 = c\\ a(x_0 + b \times t)+ b(y_0 - a \times t) = c\\ \therefore \begin{cases} x=x_0+bt\\ y=y_0-at \end{cases}$ ↩

4 证明：根据同余的定义，

a x \equiv b (\mod c)

$ax\equiv b(\mod c)$ 意味着

a x - b

$ax - b$ 能被

c

$c$ 整除，即存在整数

y

$y$ ，使得

a x - b = - c y

$ax - b = -cy$ ，移项可得

a x + c y = b

$ax + cy = b$ 。 ↩